Difference between revisions of "2021 JMPSC Sprint Problems/Problem 7"
Tigerzhang (talk | contribs) (→Solution) |
|||
| Line 8: | Line 8: | ||
~tigerzhang | ~tigerzhang | ||
| + | |||
| + | |||
| + | |||
| + | ==See also== | ||
| + | #[[2021 JMPSC Sprint Problems|Other 2021 JMPSC Sprint Problems]] | ||
| + | #[[2021 JMPSC Sprint Answer Key|2021 JMPSC Sprint Answer Key]] | ||
| + | #[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]] | ||
| + | {{JMPSC Notice}} | ||
Revision as of 16:13, 11 July 2021
Problem
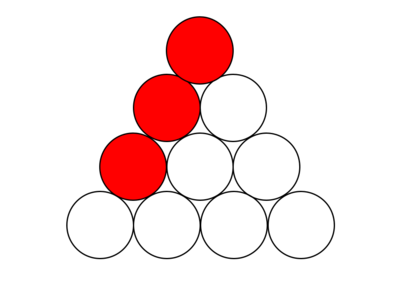
How many sets of three circles are in the diagram below such that their centers lie on the same line and each circle in the set is adjacent to another circle in the set? (Assume that if the centers of three circles appear to be on the same line, then they are on the same line. For example, the three red shaded circles count as one such set.)
Solution
Consider the equilateral triangle that the circles make. There are 
ways to pick the circles so that the row they make is parallel to each side of the equilateral triangle. Thus, there are 
ways total. [diagram needed]
~tigerzhang
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. 
