Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Incenter/excenter lemma"
m
 
(2 intermediate revisions by the same user not shown)
Line 9: Line 9:
 
Let <math>A = \angle BAC</math>, <math>B = \angle CBA</math>, <math>C = \angle ACB</math>, and note that <math>A</math>, <math>I</math>, <math>L</math> are collinear (as <math>L</math> is on the angle bisector). We are going to show that <math>LB = LI</math>, the other cases being similar.
 
Let <math>A = \angle BAC</math>, <math>B = \angle CBA</math>, <math>C = \angle ACB</math>, and note that <math>A</math>, <math>I</math>, <math>L</math> are collinear (as <math>L</math> is on the angle bisector). We are going to show that <math>LB = LI</math>, the other cases being similar.
 
First, notice that <cmath>\angle LBI = \angle LBC + \angle CBI = \angle LAC + \angle CBI = \angle IAC + \angle CBI = \frac{1}{2} A + \frac{1}{2} B.</cmath> However, <cmath>\angle BIL = \angle BAI + \angle ABI = \frac{1}{2} A + \frac{1}{2} B.</cmath> Hence, <math>\triangle BIL</math> is isosceles, so <math>LB = LI</math>. The rest of the proof proceeds along these lines. <math>\square</math>
 
First, notice that <cmath>\angle LBI = \angle LBC + \angle CBI = \angle LAC + \angle CBI = \angle IAC + \angle CBI = \frac{1}{2} A + \frac{1}{2} B.</cmath> However, <cmath>\angle BIL = \angle BAI + \angle ABI = \frac{1}{2} A + \frac{1}{2} B.</cmath> Hence, <math>\triangle BIL</math> is isosceles, so <math>LB = LI</math>. The rest of the proof proceeds along these lines. <math>\square</math>
−
 
  
 
== See also ==
 
== See also ==
 
* [[Orthic triangle]]
 
* [[Orthic triangle]]
−
* [[Geometry/Olympiad | Olympiad Geometry]]
+
* [[Geometry/Olympiad | Olympiad geometry]]
  
 
[[Category:Geometry]]
 
[[Category:Geometry]]
 
[[Category:Theorems]]
 
[[Category:Theorems]]

Latest revision as of 15:31, 18 May 2021

Diagram of the configuration.

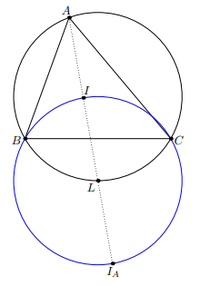
In geometry, the incenter/excenter lemma, sometimes called the Trillium theorem, is a result concerning a relationship between the incenter and excenter of a triangle. Given any $\triangle ABC$ with incenter $I$ and $A$-excenter $I_A$, let $L$ be the midpoint of $\overarc{BC}$ on the triangle's circumcenter. Then, the theorem states that $L$ is the center of a circle through $I$, $B$, $I_A$, and $C$.

The incenter/excenter lemma makes frequent appearances in olympiad geometry. Along with the larger lemma, two smaller results follow: first, $A$, $I$, $L$, and $I_A$ are collinear, and second, $I_A$ is the reflection of $I$ across $L$. Both of these follow easily from the main proof.

Proof

Let $A = \angle BAC$, $B = \angle CBA$, $C = \angle ACB$, and note that $A$, $I$, $L$ are collinear (as $L$ is on the angle bisector). We are going to show that $LB = LI$, the other cases being similar. First, notice that \[\angle LBI = \angle LBC + \angle CBI = \angle LAC + \angle CBI = \angle IAC + \angle CBI = \frac{1}{2} A + \frac{1}{2} B.\] However, \[\angle BIL = \angle BAI + \angle ABI = \frac{1}{2} A + \frac{1}{2} B.\] Hence, $\triangle BIL$ is isosceles, so $LB = LI$. The rest of the proof proceeds along these lines. $\square$

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Incenter/excenter_lemma&oldid=153885"