Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 AIME I Problems/Problem 15"

(+ prob)
 
(+ solution)
Line 2: Line 2:
 
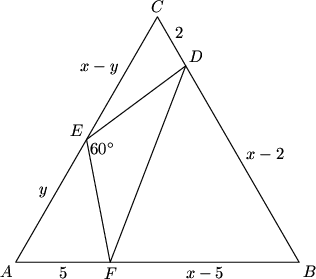
Let <math>ABC</math> be an [[equilateral triangle]], and let <math>D</math> and <math>F</math> be [[point]]s on sides <math>BC</math> and <math>AB</math>, respectively, with <math>FA = 5</math> and <math>CD = 2</math>.  Point <math>E</math> lies on side <math>CA</math> such that [[angle]] <math>DEF = 60^{\circ}</math>.  The area of triangle <math>DEF</math> is <math>14\sqrt{3}</math>.  The two possible values of the length of side <math>AB</math> are <math>p \pm q \sqrt{r}</math>, where <math>p</math> and <math>q</math> are rational, and <math>r</math> is an [[integer]] not divisible by the [[square]] of a [[prime]].  Find <math>r</math>.
 
Let <math>ABC</math> be an [[equilateral triangle]], and let <math>D</math> and <math>F</math> be [[point]]s on sides <math>BC</math> and <math>AB</math>, respectively, with <math>FA = 5</math> and <math>CD = 2</math>.  Point <math>E</math> lies on side <math>CA</math> such that [[angle]] <math>DEF = 60^{\circ}</math>.  The area of triangle <math>DEF</math> is <math>14\sqrt{3}</math>.  The two possible values of the length of side <math>AB</math> are <math>p \pm q \sqrt{r}</math>, where <math>p</math> and <math>q</math> are rational, and <math>r</math> is an [[integer]] not divisible by the [[square]] of a [[prime]].  Find <math>r</math>.
  
−
{{image}}
 
 
== Solution ==
 
== Solution ==
−
{{solution}}
+
[[Image:AIME I 2007-15.png]]
 +
 
 +
Denote the length of a side of the triangle <math>x</math>, and of <math>\overline{AE}</math> as <math>y</math>. The area of the entire equilateral triangle is <math>\frac{x^2\sqrt{3}}{4}</math>. Add up the areas of the triangles using the <math>\frac{1}{2}ab\sin C</math> formula (notice that for the three outside triangles, <math>\sin 60 = \frac{\sqrt{3}}{2}</math>): <math>\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5 \cdot y + (x - 2)(x - 5) + 2(x - y)) + 14\sqrt{3}</math>. This simplifies to <math>\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5y + x^2 - 7x + 10 + 2x - 2y + 56)</math>. Some terms will cancel out, leaving <math>y = \frac{5}{3}x - 22</math>.
 +
 
 +
<math>\angle FEC</math> is an [[external angle]] to <math>\triangle AEF</math>, from which we find that <math>\displaystyle 60 + \angle CED = 60 + \angle AFE</math>, so <math>\displaystyle \angle CED = \angle AFE</math>. Similarly, we find that <math>\angle EDC = \angle AEF</math>. Thus, <math>\triangle AEF \sim \triangle CDE</math>. Setting up a [[ratio]] of sides, we get that <math>\frac{5}{x-y} = \frac{y}{2}</math>. Using the previous relationship between <math>x</math> and <math>y</math>, we can solve for <math>x</math>.
 +
 +
<div style="text-align:center;">
 +
<math>\displaystyle xy - y^2 = 10</math>
 +
 
 +
<math>\frac{5}{3}x^2 - 22x - \left(\frac{5}{3}x - 22\right)^2 - 10 = 0</math>
 +
 
 +
<math>\frac{5}{3}x^2 - \frac{25}{9}x^2 - 22x + 2 \cdot \frac{5 \cdot 22}{3}x - 22^2 - 10= 0</math>
 +
 
 +
<math>10x^2 - 462x + 66^2 + 90 = 0</math>
 +
</div>
 +
 
 +
Use the [[quadratic formula]], though we only need the root of the [[discriminant]]. This is <math>\sqrt{(7 \cdot 66)^2 - 4 \cdot 10 \cdot (66^2 + 90)} = \sqrt{49 \cdot 66^2 - 40 \cdot 66^2 - 4 \cdot 9 \cdot 100}</math><math> = \sqrt{9 \cdot 4 \cdot 33^2 - 9 \cdot 4 \cdot 100} = 6\sqrt{33^2 - 100}</math>. The answer is <math>989</math>.
  
 
== See also ==
 
== See also ==

Revision as of 16:03, 20 March 2007

Problem

Let $ABC$ be an equilateral triangle, and let $D$ and $F$ be points on sides $BC$ and $AB$, respectively, with $FA = 5$ and $CD = 2$. Point $E$ lies on side $CA$ such that angle $DEF = 60^{\circ}$. The area of triangle $DEF$ is $14\sqrt{3}$. The two possible values of the length of side $AB$ are $p \pm q \sqrt{r}$, where $p$ and $q$ are rational, and $r$ is an integer not divisible by the square of a prime. Find $r$.

Solution

AIME I 2007-15.png

Denote the length of a side of the triangle $x$, and of $\overline{AE}$ as $y$. The area of the entire equilateral triangle is $\frac{x^2\sqrt{3}}{4}$. Add up the areas of the triangles using the $\frac{1}{2}ab\sin C$ formula (notice that for the three outside triangles, $\sin 60 = \frac{\sqrt{3}}{2}$): $\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5 \cdot y + (x - 2)(x - 5) + 2(x - y)) + 14\sqrt{3}$. This simplifies to $\frac{x^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}(5y + x^2 - 7x + 10 + 2x - 2y + 56)$. Some terms will cancel out, leaving $y = \frac{5}{3}x - 22$.

$\angle FEC$ is an external angle to $\triangle AEF$, from which we find that $\displaystyle 60 + \angle CED = 60 + \angle AFE$, so $\displaystyle \angle CED = \angle AFE$. Similarly, we find that $\angle EDC = \angle AEF$. Thus, $\triangle AEF \sim \triangle CDE$. Setting up a ratio of sides, we get that $\frac{5}{x-y} = \frac{y}{2}$. Using the previous relationship between $x$ and $y$, we can solve for $x$.

$\displaystyle xy - y^2 = 10$

$\frac{5}{3}x^2 - 22x - \left(\frac{5}{3}x - 22\right)^2 - 10 = 0$

$\frac{5}{3}x^2 - \frac{25}{9}x^2 - 22x + 2 \cdot \frac{5 \cdot 22}{3}x - 22^2 - 10= 0$

$10x^2 - 462x + 66^2 + 90 = 0$

Use the quadratic formula, though we only need the root of the discriminant. This is $\sqrt{(7 \cdot 66)^2 - 4 \cdot 10 \cdot (66^2 + 90)} = \sqrt{49 \cdot 66^2 - 40 \cdot 66^2 - 4 \cdot 9 \cdot 100}$$= \sqrt{9 \cdot 4 \cdot 33^2 - 9 \cdot 4 \cdot 100} = 6\sqrt{33^2 - 100}$. The answer is $989$.

See also

2007 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_AIME_I_Problems/Problem_15&oldid=14119"