Difference between revisions of "1990 AIME Problems/Problem 14"
m |
|||
| Line 1: | Line 1: | ||
| − | |||
== Problem == | == Problem == | ||
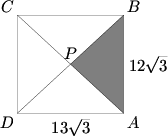
| + | The rectangle <math>ABCD^{}_{}</math> below has dimensions <math>AB^{}_{} = 12 \sqrt{3}</math> and <math>BC^{}_{} = 13 \sqrt{3}</math>. Diagonals <math>\overline{AC}</math> and <math>\overline{BD}</math> intersect at <math>P^{}_{}</math>. If triangle <math>ABP^{}_{}</math> is cut out and removed, edges <math>\overline{AP}</math> and <math>\overline{BP}</math> are joined, and the figure is then creased along segments <math>\overline{CP}</math> and <math>\overline{DP}</math>, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid. | ||
| + | |||
| + | [[Image:AIME_1990_Problem_14.png]] | ||
== Solution == | == Solution == | ||
{{solution}} | {{solution}} | ||
| + | |||
== See also == | == See also == | ||
| − | + | {{AIME box|year=1990|num-b=13|num-a=15}} | |
Revision as of 00:46, 2 March 2007
Problem
The rectangle 
below has dimensions 
and 
. Diagonals 
and 
intersect at 
. If triangle 
is cut out and removed, edges 
and 
are joined, and the figure is then creased along segments 
and 
, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
See also
| 1990 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
