Difference between revisions of "1985 AIME Problems/Problem 4"
(→Problem) |
|||
| (10 intermediate revisions by 7 users not shown) | |||
| Line 4: | Line 4: | ||
[[Image:AIME_1985_Problem_4.png]] | [[Image:AIME_1985_Problem_4.png]] | ||
| − | == Solution == | + | == Solution 1== |
| − | The lines passing through <math>A</math> and <math>C</math> divide the square into three parts, two [[right triangle]]s and a [[parallelogram]]. | + | The lines passing through <math>A</math> and <math>C</math> divide the square into three parts, two [[right triangle]]s and a [[parallelogram]]. Using the smaller side of the parallelogram, <math>1/n</math>, as the base, where the height is 1, we find that the area of the parallelogram is <math>A = \frac{1}{n}</math>. By the [[Pythagorean Theorem]], the longer base of the parallelogram has [[length]] <math>l = \sqrt{1^2 + \left(\frac{n - 1}{n}\right)^2} = \frac{1}{n}\sqrt{2n^2 - 2n + 1}</math>, so the parallelogram has height <math>h = \frac{A}{l} = \frac{1}{\sqrt{2n^2 - 2n + 1}}</math>. But the height of the parallelogram is the side of the little square, so <math>2n^2 - 2n + 1 = 1985</math>. Solving this [[quadratic equation]] gives <math>n = \boxed{32}</math>. |
| + | |||
| + | ==Solution 2== | ||
| + | [[File:Aime.png]] | ||
| + | |||
| + | Surrounding the square with area <math>\frac{1}{1985}</math> are <math>4</math> right triangles with hypotenuse <math>1</math> (sides of the large square). Thus, <math>X + \frac{1}{1985} = 1</math>, where <math>X</math> is the area of the of the 4 triangles. | ||
| + | We can thus use proportions to solve this problem. | ||
| + | <cmath>\begin{eqnarray*} | ||
| + | \frac{GF}{BE}=\frac{CG}{CB}\implies | ||
| + | \frac{\frac{1}{\sqrt{1985}}}{BE}=\frac{\frac{1}{n}}{1}\implies | ||
| + | BE=\frac{n\sqrt{1985}}{1985} | ||
| + | \end{eqnarray*}</cmath> | ||
| + | Also, | ||
| + | <cmath>\begin{eqnarray*} | ||
| + | \frac{BE}{1}=\frac{EC}{\frac{n-1}{n}}\implies | ||
| + | EC=\frac{\sqrt{1985}}{1985}(n-1) | ||
| + | \end{eqnarray*}</cmath> | ||
| + | Thus, | ||
| + | <cmath>\begin{eqnarray*} | ||
| + | 2(BE)(EC)+\frac{1}{1985}=1\\ | ||
| + | 2n^{2}-2n+1=1985\\ | ||
| + | n(n-1)=992 | ||
| + | \end{eqnarray*}</cmath> | ||
| + | Simple factorization and guess and check gives us <math>\boxed{32}</math>. | ||
| + | |||
| + | == Solution 3 == | ||
| + | [[File:AIME_1985_Problem_4_Solution_3_Diagram.png]] | ||
| + | |||
| + | Line Segment <math>DE = \frac{1}{n}</math>, so <math>EC = 1 - \frac{1}{n} = \frac{n-1}{n}</math>. Draw line segment <math>HE</math> parallel to the corresponding sides of the small square, <math>HE</math> has length <math>\frac{1}{\sqrt{1985}}</math>, as it is the same length as the sides of the square. Notice that <math>\triangle CEL</math> is similar to <math>\triangle HDE</math> by <math>AA</math> similarity. Thus, <math>\frac{LC}{HE} = \frac{EC}{DE} = n-1</math>, so <math>LC = \frac{n-1}{\sqrt{1985}}</math>. Notice that <math>\triangle CEL</math> is also similar to <math>\triangle CDF</math> by <math>AA</math> similarity. Thus, <math>\frac{FC}{EC} = \frac{DC}{LC}</math>, and the expression simplifies into a quadratic equation <math>n^2 - n - 992 = 0</math>. Solving this quadratic equation yields <math>n =\boxed{32}</math>. | ||
== See also == | == See also == | ||
Latest revision as of 20:40, 2 March 2020
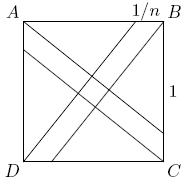
Problem
A small square is constructed inside a square of area 1 by dividing each side of the unit square into ![]() equal parts, and then connecting the vertices to the division points closest to the opposite vertices. Find the value of
equal parts, and then connecting the vertices to the division points closest to the opposite vertices. Find the value of ![]() if the the area of the small square is exactly
if the the area of the small square is exactly ![]() .
.
Solution 1
The lines passing through ![]() and
and ![]() divide the square into three parts, two right triangles and a parallelogram. Using the smaller side of the parallelogram,
divide the square into three parts, two right triangles and a parallelogram. Using the smaller side of the parallelogram, ![]() , as the base, where the height is 1, we find that the area of the parallelogram is
, as the base, where the height is 1, we find that the area of the parallelogram is ![]() . By the Pythagorean Theorem, the longer base of the parallelogram has length
. By the Pythagorean Theorem, the longer base of the parallelogram has length  , so the parallelogram has height
, so the parallelogram has height ![]() . But the height of the parallelogram is the side of the little square, so
. But the height of the parallelogram is the side of the little square, so ![]() . Solving this quadratic equation gives
. Solving this quadratic equation gives ![]() .
.
Solution 2
Surrounding the square with area ![]() are
are ![]() right triangles with hypotenuse
right triangles with hypotenuse ![]() (sides of the large square). Thus,
(sides of the large square). Thus, ![]() , where
, where ![]() is the area of the of the 4 triangles.
We can thus use proportions to solve this problem.
is the area of the of the 4 triangles.
We can thus use proportions to solve this problem.
![]() Also,
Also,
![]() Thus,
Thus,
 Simple factorization and guess and check gives us
Simple factorization and guess and check gives us ![]() .
.
Solution 3
Line Segment ![]() , so
, so ![]() . Draw line segment
. Draw line segment ![]() parallel to the corresponding sides of the small square,
parallel to the corresponding sides of the small square, ![]() has length
has length ![]() , as it is the same length as the sides of the square. Notice that
, as it is the same length as the sides of the square. Notice that ![]() is similar to
is similar to ![]() by
by ![]() similarity. Thus,
similarity. Thus, ![]() , so
, so ![]() . Notice that
. Notice that ![]() is also similar to
is also similar to ![]() by
by ![]() similarity. Thus,
similarity. Thus, ![]() , and the expression simplifies into a quadratic equation
, and the expression simplifies into a quadratic equation ![]() . Solving this quadratic equation yields
. Solving this quadratic equation yields ![]() .
.
See also
| 1985 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||