Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
GET READY FOR THE AMC 12 WITH AoPS
Learn with outstanding instructors and top-scoring students from around the world in our AMC 12 Problem Series online course.
CHECK SCHEDULE

Difference between revisions of "2002 AMC 12A Problems"

(Set up the page.)
 
m
 
(32 intermediate revisions by 15 users not shown)
Line 1: Line 1:
 +
{{AMC12 Problems|year=2002|ab=A}}
 
== Problem 1 ==
 
== Problem 1 ==
  
−
[[2002 AMC 12A Problem 1|Solution]]
+
Compute the sum of all the roots of
 +
<math>(2x+3)(x-4)+(2x+3)(x-6)=0 </math>
 +
 
 +
<math> \mathrm{(A) \ } \frac{7}{2}\qquad \mathrm{(B) \ } 4\qquad \mathrm{(C) \ } 5\qquad \mathrm{(D) \ } 7\qquad \mathrm{(E) \ } 13 </math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 1|Solution]]
  
 
== Problem 2 ==
 
== Problem 2 ==
  
−
[[2002 AMC 12A Problem 2|Solution]]
+
Cindy was asked by her teacher to subtract 3 from a certain number and then divide the result by 9. Instead, she subtracted 9 and then divided the result by 3, giving an answer of 43. What would her answer have been had she worked the problem correctly?
 +
 
 +
<math> \mathrm{(A) \ } 15\qquad \mathrm{(B) \ } 34\qquad \mathrm{(C) \ } 43\qquad \mathrm{(D) \ } 51\qquad \mathrm{(E) \ } 138 </math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 2|Solution]]
  
 
== Problem 3 ==
 
== Problem 3 ==
 +
According to the standard convention for exponentiation,
 +
<cmath> 2^{2^{2^{2}}} = 2^{\left(2^{\left(2^2\right)}\right)} = 2^{16} = 65536. </cmath>
  
−
[[2002 AMC 12A Problem 3|Solution]]
+
If the order in which the exponentiations are performed is changed, how many other values are possible?
 +
 
 +
<math> \mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 1\qquad \mathrm{(C) \ } 2\qquad \mathrm{(D) \ } 3\qquad \mathrm{(E) \ } 4 </math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 3|Solution]]
  
 
== Problem 4 ==
 
== Problem 4 ==
  
−
[[2002 AMC 12A Problem 4|Solution]]
+
Find the degree measure of an angle whose complement is 25% of its supplement.
 +
 
 +
<math> \mathrm{(A) \ 48 } \qquad \mathrm{(B) \ 60 } \qquad \mathrm{(C) \ 75 } \qquad \mathrm{(D) \ 120 } \qquad \mathrm{(E) \ 150 }  </math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 4|Solution]]
  
 
== Problem 5 ==
 
== Problem 5 ==
 +
Each of the small circles in the figure has radius one. The innermost circle is tangent to the six circles that surround it, and each of those circles is tangent to the large circle and to its small-circle neighbors. Find the area of the shaded region.
 +
 +
<asy>
 +
import graph;
 +
unitsize(.3cm);
 +
path c=Circle((0,2),1);
 +
filldraw(Circle((0,0),3),grey,black);
 +
filldraw(Circle((0,0),1),white,black);
 +
filldraw(c,white,black);
 +
filldraw(rotate(60)*c,white,black);
 +
filldraw(rotate(120)*c,white,black);
 +
filldraw(rotate(180)*c,white,black);
 +
filldraw(rotate(240)*c,white,black);
 +
filldraw(rotate(300)*c,white,black);
 +
</asy>
 +
 +
<math>\text{(A)}\ \pi \qquad \text{(B)}\ 1.5\pi \qquad \text{(C)}\ 2\pi \qquad \text{(D)}\ 3\pi \qquad \text{(E)}\ 3.5\pi</math>
  
−
[[2002 AMC 12A Problem 5|Solution]]
+
[[2002 AMC 12A Problems/Problem 5|Solution]]
  
 
== Problem 6 ==
 
== Problem 6 ==
 +
For how many positive integers <math>m</math> does there exist at least one positive integer <math>n</math> such that <math>m \cdot n \le m + n</math>?
  
−
[[2002 AMC 12A Problem 6|Solution]]
+
<math> \mathrm{(A) \ } 4\qquad \mathrm{(B) \ } 6\qquad \mathrm{(C) \ } 9\qquad \mathrm{(D) \ } 12\qquad \mathrm{(E) \ }</math>  infinitely many
 +
 
 +
[[2002 AMC 12A Problems/Problem 6|Solution]]
  
 
== Problem 7 ==
 
== Problem 7 ==
  
−
[[2002 AMC 12A Problem 7|Solution]]
+
A <math>45^\circ</math> arc of circle A is equal in length to a <math>30^\circ</math> arc of circle B. What is the ratio of circle A's area and circle B's area?
 +
 
 +
<math>\text{(A)}\ 4/9 \qquad \text{(B)}\ 2/3 \qquad \text{(C)}\ 5/6 \qquad \text{(D)}\ 3/2 \qquad \text{(E)}\ 9/4</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 7|Solution]]
  
 
== Problem 8 ==
 
== Problem 8 ==
 +
Betsy designed a flag using blue triangles, small white squares, and a red center square, as shown. Let <math>B</math> be the total area of the blue triangles, <math>W</math> the total area of the white squares, and <math>R</math> the area of the red square. Which of the following is correct?
  
−
[[2002 AMC 12A Problem 8|Solution]]
+
<asy>
 +
unitsize(3mm);
 +
fill((-4,-4)--(-4,4)--(4,4)--(4,-4)--cycle,blue);
 +
fill((-2,-2)--(-2,2)--(2,2)--(2,-2)--cycle,red);
 +
path onewhite=(-3,3)--(-2,4)--(-1,3)--(-2,2)--(-3,3)--(-1,3)--(0,4)--(1,3)--(0,2)--(-1,3)--(1,3)--(2,4)--(3,3)--(2,2)--(1,3)--cycle;
 +
path divider=(-2,2)--(-3,3)--cycle;
 +
fill(onewhite,white);
 +
fill(rotate(90)*onewhite,white);
 +
fill(rotate(180)*onewhite,white);
 +
fill(rotate(270)*onewhite,white);
 +
</asy>
 +
 +
<math>\text{(A)}\ B = W \qquad \text{(B)}\ W = R \qquad \text{(C)}\ B = R \qquad \text{(D)}\ 3B = 2R \qquad \text{(E)}\ 2R = W</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 8|Solution]]
  
 
== Problem 9 ==
 
== Problem 9 ==
  
−
[[2002 AMC 12A Problem 9|Solution]]
+
Jamal wants to save 30 files onto disks, each with 1.44 MB space. 3 of the files take up 0.8 MB, 12 of the files take up 0.7 MB, and the rest take up 0.4 MB. It is not possible to split a file onto 2 different disks. What is the smallest number of disks needed to store all 30 files?
 +
 
 +
<math>\text{(A)}\ 12 \qquad \text{(B)}\ 13 \qquad \text{(C)}\ 14 \qquad \text{(D)}\ 15 \qquad \text{(E)} 16</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 9|Solution]]
  
 
== Problem 10 ==
 
== Problem 10 ==
 +
Sarah places four ounces of coffee into an eight-ounce cup and four ounces of cream into a second cup of the same size. She then pours half the coffee from the first cup to the second and, after stirring thoroughly, pours half the liquid in the second cup back to the first. What fraction of the liquid in the first cup is now cream?
 +
 +
<math> \mathrm{(A) \ } \frac{1}{4}\qquad \mathrm{(B) \ } \frac13\qquad \mathrm{(C) \ } \frac38\qquad \mathrm{(D) \ } \frac25\qquad \mathrm{(E) \ } \frac12 </math>
  
−
[[2002 AMC 12A Problem 10|Solution]]
+
[[2002 AMC 12A Problems/Problem 10|Solution]]
  
 
== Problem 11 ==
 
== Problem 11 ==
  
−
[[2002 AMC 12A Problem 11|Solution]]
+
Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?
 +
 
 +
<math>\text{(A)}\ 45 \qquad \text{(B)}\ 48 \qquad \text{(C)}\ 50 \qquad \text{(D)}\ 55 \qquad \text{(E)} 58</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 11|Solution]]
  
 
== Problem 12 ==
 
== Problem 12 ==
  
−
[[2002 AMC 12A Problem 12|Solution]]
+
Both roots of the quadratic equation <math>x^2 - 63x + k = 0</math> are prime numbers. The number of possible values of <math>k</math> is
 +
 
 +
<math>\text{(A)}\ 0 \qquad \text{(B)}\ 1 \qquad \text{(C)}\ 2 \qquad \text{(D)}\ 4 \qquad \text{(E) more than 4}</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 12|Solution]]
  
 
== Problem 13 ==
 
== Problem 13 ==
  
−
[[2002 AMC 12A Problem 13|Solution]]
+
Two different positive numbers <math>a</math> and <math>b</math> each differ from their reciprocals by <math>1</math>. What is <math>a+b</math>?
 +
 
 +
<math>
 +
\text{(A) }1
 +
\qquad
 +
\text{(B) }2
 +
\qquad
 +
\text{(C) }\sqrt 5
 +
\qquad
 +
\text{(D) }\sqrt 6
 +
\qquad
 +
\text{(E) }3
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 13|Solution]]
  
 
== Problem 14 ==
 
== Problem 14 ==
  
−
[[2002 AMC 12A Problem 14|Solution]]
+
For all positive integers <math>n</math>, let <math>f(n)=\log_{2002} n^2</math>. Let <math>N=f(11)+f(13)+f(14)</math>. Which of the following relations is true?
 +
 
 +
<math>
 +
\text{(A) }N<1
 +
\qquad
 +
\text{(B) }N=1
 +
\qquad
 +
\text{(C) }1<N<2
 +
\qquad
 +
\text{(D) }N=2
 +
\qquad
 +
\text{(E) }N>2
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 14|Solution]]
  
 
== Problem 15 ==
 
== Problem 15 ==
  
−
[[2002 AMC 12A Problem 15|Solution]]
+
The mean, median, unique mode, and range of a collection of eight integers are all equal to 8. The largest integer that can be an element of this collection is
 +
 
 +
<math>
 +
\text{(A) }11
 +
\qquad
 +
\text{(B) }12
 +
\qquad
 +
\text{(C) }13
 +
\qquad
 +
\text{(D) }14
 +
\qquad
 +
\text{(E) }15
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 15|Solution]]
  
 
== Problem 16 ==
 
== Problem 16 ==
  
−
[[2002 AMC 12A Problem 16|Solution]]
+
Tina randomly selects two distinct numbers from the set <math>\{1, 2, 3, 4, 5\}</math>, and Sergio randomly selects a number from the set <math>\{1, 2, \ldots, 10\}</math>. What is the probability that Sergio's number is larger than the sum of the two numbers chosen by Tina?
 +
 
 +
<math>\text{(A)}\ 2/5 \qquad \text{(B)}\ 9/20 \qquad \text{(C)}\ 1/2 \qquad \text{(D)}\ 11/20 \qquad \text{(E)}\ 24/25</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 16|Solution]]
  
 
== Problem 17 ==
 
== Problem 17 ==
  
−
[[2002 AMC 12A Problem 17|Solution]]
+
Several sets of prime numbers, such as <math>\{7,83,421,659\}</math> use each of the nine nonzero digits exactly once. What is the smallest possible sum such a set of primes could have?
 +
 
 +
<math>
 +
\text{(A) }193
 +
\qquad
 +
\text{(B) }207
 +
\qquad
 +
\text{(C) }225
 +
\qquad
 +
\text{(D) }252
 +
\qquad
 +
\text{(E) }447
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 17|Solution]]
  
 
== Problem 18 ==
 
== Problem 18 ==
 +
Let <math>C_1</math> and <math>C_2</math> be circles defined by <math>(x-10)^2 + y^2 = 36</math> and <math>(x+15)^2 + y^2 = 81</math>
 +
respectively. What is the length of the shortest line segment <math>PQ</math> that is tangent to <math>C_1</math> at <math>P</math> and to <math>C_2</math> at <math>Q</math>?
  
−
[[2002 AMC 12A Problem 18|Solution]]
+
<math>
 +
\text{(A) }15
 +
\qquad
 +
\text{(B) }18
 +
\qquad
 +
\text{(C) }20
 +
\qquad
 +
\text{(D) }21
 +
\qquad
 +
\text{(E) }24
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 18|Solution]]
  
 
== Problem 19 ==
 
== Problem 19 ==
  
−
[[2002 AMC 12A Problem 19|Solution]]
+
The graph of the function <math>f</math> is shown below. How many solutions does the equation <math>f(f(x))=6</math> have?
 +
 
 +
<asy>
 +
import graph;
 +
size(200);
 +
defaultpen(fontsize(10pt)+linewidth(.8pt));
 +
dotfactor=4;
 +
 
 +
pair P1=(-7,-4), P2=(-2,6), P3=(0,0), P4=(1,6), P5=(5,-6);
 +
real[] xticks={-7,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6};
 +
real[] yticks={-6,-5,-4,-3,-2,-1,1,2,3,4,5,6};
 +
 
 +
draw(P1--P2--P3--P4--P5);
 +
 
 +
dot("(-7, -4)",P1);
 +
dot("(-2, 6)",P2,LeftSide);
 +
dot("(1, 6)",P4);
 +
dot("(5, -6)",P5);
 +
 
 +
xaxis("$x$",-7.5,7,Ticks(xticks),EndArrow(6));
 +
yaxis("$y$",-6.5,7,Ticks(yticks),EndArrow(6));
 +
</asy>
 +
 
 +
<math>
 +
\text{(A) }2
 +
\qquad
 +
\text{(B) }4
 +
\qquad
 +
\text{(C) }5
 +
\qquad
 +
\text{(D) }6
 +
\qquad
 +
\text{(E) }7
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 19|Solution]]
  
 
== Problem 20 ==
 
== Problem 20 ==
  
−
[[2002 AMC 12A Problem 20|Solution]]
+
Suppose that <math>a</math> and <math>b</math> are digits, not both nine and not both zero, and the repeating decimal <math>0.\overline{ab}</math> is expressed as a fraction in lowest terms. How many different denominators are possible?
 +
 
 +
<math>
 +
\text{(A) }3
 +
\qquad
 +
\text{(B) }4
 +
\qquad
 +
\text{(C) }5
 +
\qquad
 +
\text{(D) }8
 +
\qquad
 +
\text{(E) }9
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 20|Solution]]
  
 
== Problem 21 ==
 
== Problem 21 ==
  
−
[[2002 AMC 12A Problem 21|Solution]]
+
Consider the sequence of numbers: <math>4,7,1,8,9,7,6,\dots</math> For <math>n>2</math>, the <math>n</math>-th term of the sequence is the units digit of the sum of the two previous terms. Let <math>S_n</math> denote the sum of the first <math>n</math> terms of this sequence. The smallest value of <math>n</math> for which <math>S_n>10,000</math> is:
 +
 
 +
<math>
 +
\text{(A) }1992
 +
\qquad
 +
\text{(B) }1999
 +
\qquad
 +
\text{(C) }2001
 +
\qquad
 +
\text{(D) }2002
 +
\qquad
 +
\text{(E) }2004
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 21|Solution]]
  
 
== Problem 22 ==
 
== Problem 22 ==
  
−
[[2002 AMC 12A Problem 22|Solution]]
+
Triangle <math>ABC</math> is a right triangle with <math>\angle ACB</math> as its right angle, <math>m\angle ABC = 60^{\circ}</math>, and <math>AB = 10</math>. Let <math>P</math> be randomly chosen inside <math>\triangle ABC</math>, and extend <math>\overline{BP}</math> to meet <math>\overline{AC}</math> at <math>D</math>. What is the probability that <math>BD > 5\sqrt{2}</math>?
 +
 
 +
<math> \textbf{(A)}\ \frac{2-\sqrt2}{2}\qquad\textbf{(B)}\ \frac{1}{3}\qquad\textbf{(C)}\ \frac{3-\sqrt3}{3}\qquad\textbf{(D)}\ \frac{1}{2}\qquad\textbf{(E)}\ \frac{5-\sqrt5}{5} </math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 22|Solution]]
  
 
== Problem 23 ==
 
== Problem 23 ==
 +
In triangle <math>ABC</math>, side <math>AC</math> and the perpendicular bisector of <math>BC</math> meet in point <math>D</math>, and <math>BD</math> bisects <math>\angle ABC</math>.  If <math>AD = 9</math> and <math>DC = 7</math>, what is the area of triangle <math>ABD</math>?
  
−
[[2002 AMC 12A Problem 23|Solution]]
+
<math>\text{(A)}\ 14 \qquad \text{(B)}\ 21 \qquad \text{(C)}\ 28 \qquad \text{(D)}\ 14\sqrt5 \qquad \text{(E)}\ 28\sqrt5</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 23|Solution]]
  
 
== Problem 24 ==
 
== Problem 24 ==
  
−
[[2002 AMC 12A Problem 24|Solution]]
+
Find the number of ordered pairs of real numbers <math>(a,b)</math> such that <math>(a+bi)^{2002} = a-bi</math>.
 +
 
 +
<math>
 +
\text{(A) }1001
 +
\qquad
 +
\text{(B) }1002
 +
\qquad
 +
\text{(C) }2001
 +
\qquad
 +
\text{(D) }2002
 +
\qquad
 +
\text{(E) }2004
 +
</math>
 +
 
 +
[[2002 AMC 12A Problems/Problem 24|Solution]]
  
 
== Problem 25 ==
 
== Problem 25 ==
  
−
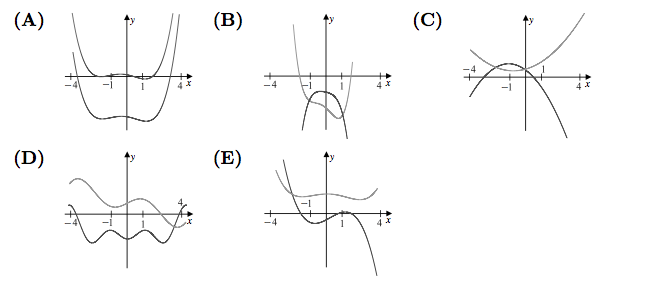
[[2002 AMC 12A Problem 25|Solution]]
+
The nonzero coefficients of a polynomial <math>P</math> with real coefficients are all replaced by their mean to form a polynomial <math>Q</math>. Which of the following could be a graph of <math>y = P(x)</math> and <math>y = Q(x)</math> over the interval <math>-4\leq x \leq 4</math>?
 +
 
 +
[[File:2002AMC12A25.png]]
 +
 
 +
[[2002 AMC 12A Problems/Problem 25|Solution]]
  
 
== See also ==
 
== See also ==
 +
 +
{{AMC12 box|year=2002|ab=A|before=[[2001 AMC 12 Problems]]|after=[[2002 AMC 12B Problems]]}}
 +
 
* [[AMC 12]]
 
* [[AMC 12]]
 
* [[AMC 12 Problems and Solutions]]
 
* [[AMC 12 Problems and Solutions]]
 
* [[2002 AMC 12A]]
 
* [[2002 AMC 12A]]
 
* [[Mathematics competition resources]]
 
* [[Mathematics competition resources]]
 +
 +
{{MAA Notice}}

Latest revision as of 12:06, 19 February 2020

2002 AMC 12A (Answer Key)
Printable versions: Wiki • AoPS Resources • PDF

Instructions

  1. This is a 25-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct.
  2. You will receive 6 points for each correct answer, 2.5 points for each problem left unanswered if the year is before 2006, 1.5 points for each problem left unanswered if the year is after 2006, and 0 points for each incorrect answer.
  3. No aids are permitted other than scratch paper, graph paper, ruler, compass, protractor and erasers (and calculators that are accepted for use on the test if before 2006. No problems on the test will require the use of a calculator).
  4. Figures are not necessarily drawn to scale.
  5. You will have 75 minutes working time to complete the test.
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25

Problem 1

Compute the sum of all the roots of $(2x+3)(x-4)+(2x+3)(x-6)=0$

$\mathrm{(A) \ } \frac{7}{2}\qquad \mathrm{(B) \ } 4\qquad \mathrm{(C) \ } 5\qquad \mathrm{(D) \ } 7\qquad \mathrm{(E) \ } 13$

Solution

Problem 2

Cindy was asked by her teacher to subtract 3 from a certain number and then divide the result by 9. Instead, she subtracted 9 and then divided the result by 3, giving an answer of 43. What would her answer have been had she worked the problem correctly?

$\mathrm{(A) \ } 15\qquad \mathrm{(B) \ } 34\qquad \mathrm{(C) \ } 43\qquad \mathrm{(D) \ } 51\qquad \mathrm{(E) \ } 138$

Solution

Problem 3

According to the standard convention for exponentiation, \[2^{2^{2^{2}}} = 2^{\left(2^{\left(2^2\right)}\right)} = 2^{16} = 65536.\]

If the order in which the exponentiations are performed is changed, how many other values are possible?

$\mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 1\qquad \mathrm{(C) \ } 2\qquad \mathrm{(D) \ } 3\qquad \mathrm{(E) \ } 4$

Solution

Problem 4

Find the degree measure of an angle whose complement is 25% of its supplement.

$\mathrm{(A) \ 48 } \qquad \mathrm{(B) \ 60 } \qquad \mathrm{(C) \ 75 } \qquad \mathrm{(D) \ 120 } \qquad \mathrm{(E) \ 150 }$

Solution

Problem 5

Each of the small circles in the figure has radius one. The innermost circle is tangent to the six circles that surround it, and each of those circles is tangent to the large circle and to its small-circle neighbors. Find the area of the shaded region.

[asy] import graph; unitsize(.3cm); path c=Circle((0,2),1); filldraw(Circle((0,0),3),grey,black); filldraw(Circle((0,0),1),white,black); filldraw(c,white,black); filldraw(rotate(60)*c,white,black); filldraw(rotate(120)*c,white,black); filldraw(rotate(180)*c,white,black); filldraw(rotate(240)*c,white,black); filldraw(rotate(300)*c,white,black); [/asy]

$\text{(A)}\ \pi \qquad \text{(B)}\ 1.5\pi \qquad \text{(C)}\ 2\pi \qquad \text{(D)}\ 3\pi \qquad \text{(E)}\ 3.5\pi$

Solution

Problem 6

For how many positive integers $m$ does there exist at least one positive integer $n$ such that $m \cdot n \le m + n$?

$\mathrm{(A) \ } 4\qquad \mathrm{(B) \ } 6\qquad \mathrm{(C) \ } 9\qquad \mathrm{(D) \ } 12\qquad \mathrm{(E) \ }$ infinitely many

Solution

Problem 7

A $45^\circ$ arc of circle A is equal in length to a $30^\circ$ arc of circle B. What is the ratio of circle A's area and circle B's area?

$\text{(A)}\ 4/9 \qquad \text{(B)}\ 2/3 \qquad \text{(C)}\ 5/6 \qquad \text{(D)}\ 3/2 \qquad \text{(E)}\ 9/4$

Solution

Problem 8

Betsy designed a flag using blue triangles, small white squares, and a red center square, as shown. Let $B$ be the total area of the blue triangles, $W$ the total area of the white squares, and $R$ the area of the red square. Which of the following is correct?

[asy] unitsize(3mm); fill((-4,-4)--(-4,4)--(4,4)--(4,-4)--cycle,blue); fill((-2,-2)--(-2,2)--(2,2)--(2,-2)--cycle,red); path onewhite=(-3,3)--(-2,4)--(-1,3)--(-2,2)--(-3,3)--(-1,3)--(0,4)--(1,3)--(0,2)--(-1,3)--(1,3)--(2,4)--(3,3)--(2,2)--(1,3)--cycle; path divider=(-2,2)--(-3,3)--cycle; fill(onewhite,white); fill(rotate(90)*onewhite,white); fill(rotate(180)*onewhite,white); fill(rotate(270)*onewhite,white); [/asy]

$\text{(A)}\ B = W \qquad \text{(B)}\ W = R \qquad \text{(C)}\ B = R \qquad \text{(D)}\ 3B = 2R \qquad \text{(E)}\ 2R = W$

Solution

Problem 9

Jamal wants to save 30 files onto disks, each with 1.44 MB space. 3 of the files take up 0.8 MB, 12 of the files take up 0.7 MB, and the rest take up 0.4 MB. It is not possible to split a file onto 2 different disks. What is the smallest number of disks needed to store all 30 files?

$\text{(A)}\ 12 \qquad \text{(B)}\ 13 \qquad \text{(C)}\ 14 \qquad \text{(D)}\ 15 \qquad \text{(E)} 16$

Solution

Problem 10

Sarah places four ounces of coffee into an eight-ounce cup and four ounces of cream into a second cup of the same size. She then pours half the coffee from the first cup to the second and, after stirring thoroughly, pours half the liquid in the second cup back to the first. What fraction of the liquid in the first cup is now cream?

$\mathrm{(A) \ } \frac{1}{4}\qquad \mathrm{(B) \ } \frac13\qquad \mathrm{(C) \ } \frac38\qquad \mathrm{(D) \ } \frac25\qquad \mathrm{(E) \ } \frac12$

Solution

Problem 11

Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?

$\text{(A)}\ 45 \qquad \text{(B)}\ 48 \qquad \text{(C)}\ 50 \qquad \text{(D)}\ 55 \qquad \text{(E)} 58$

Solution

Problem 12

Both roots of the quadratic equation $x^2 - 63x + k = 0$ are prime numbers. The number of possible values of $k$ is

$\text{(A)}\ 0 \qquad \text{(B)}\ 1 \qquad \text{(C)}\ 2 \qquad \text{(D)}\ 4 \qquad \text{(E) more than 4}$

Solution

Problem 13

Two different positive numbers $a$ and $b$ each differ from their reciprocals by $1$. What is $a+b$?

$\text{(A) }1 \qquad \text{(B) }2 \qquad \text{(C) }\sqrt 5 \qquad \text{(D) }\sqrt 6 \qquad \text{(E) }3$

Solution

Problem 14

For all positive integers $n$, let $f(n)=\log_{2002} n^2$. Let $N=f(11)+f(13)+f(14)$. Which of the following relations is true?

$\text{(A) }N<1 \qquad \text{(B) }N=1 \qquad \text{(C) }1<N<2 \qquad \text{(D) }N=2 \qquad \text{(E) }N>2$

Solution

Problem 15

The mean, median, unique mode, and range of a collection of eight integers are all equal to 8. The largest integer that can be an element of this collection is

$\text{(A) }11 \qquad \text{(B) }12 \qquad \text{(C) }13 \qquad \text{(D) }14 \qquad \text{(E) }15$

Solution

Problem 16

Tina randomly selects two distinct numbers from the set $\{1, 2, 3, 4, 5\}$, and Sergio randomly selects a number from the set $\{1, 2, \ldots, 10\}$. What is the probability that Sergio's number is larger than the sum of the two numbers chosen by Tina?

$\text{(A)}\ 2/5 \qquad \text{(B)}\ 9/20 \qquad \text{(C)}\ 1/2 \qquad \text{(D)}\ 11/20 \qquad \text{(E)}\ 24/25$

Solution

Problem 17

Several sets of prime numbers, such as $\{7,83,421,659\}$ use each of the nine nonzero digits exactly once. What is the smallest possible sum such a set of primes could have?

$\text{(A) }193 \qquad \text{(B) }207 \qquad \text{(C) }225 \qquad \text{(D) }252 \qquad \text{(E) }447$

Solution

Problem 18

Let $C_1$ and $C_2$ be circles defined by $(x-10)^2 + y^2 = 36$ and $(x+15)^2 + y^2 = 81$ respectively. What is the length of the shortest line segment $PQ$ that is tangent to $C_1$ at $P$ and to $C_2$ at $Q$?

$\text{(A) }15 \qquad \text{(B) }18 \qquad \text{(C) }20 \qquad \text{(D) }21 \qquad \text{(E) }24$

Solution

Problem 19

The graph of the function $f$ is shown below. How many solutions does the equation $f(f(x))=6$ have?

[asy] import graph; size(200); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=4; pair P1=(-7,-4), P2=(-2,6), P3=(0,0), P4=(1,6), P5=(5,-6); real[] xticks={-7,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; real[] yticks={-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; draw(P1--P2--P3--P4--P5); dot("(-7, -4)",P1); dot("(-2, 6)",P2,LeftSide); dot("(1, 6)",P4); dot("(5, -6)",P5); xaxis("$x$",-7.5,7,Ticks(xticks),EndArrow(6)); yaxis("$y$",-6.5,7,Ticks(yticks),EndArrow(6)); [/asy]

$\text{(A) }2 \qquad \text{(B) }4 \qquad \text{(C) }5 \qquad \text{(D) }6 \qquad \text{(E) }7$

Solution

Problem 20

Suppose that $a$ and $b$ are digits, not both nine and not both zero, and the repeating decimal $0.\overline{ab}$ is expressed as a fraction in lowest terms. How many different denominators are possible?

$\text{(A) }3 \qquad \text{(B) }4 \qquad \text{(C) }5 \qquad \text{(D) }8 \qquad \text{(E) }9$

Solution

Problem 21

Consider the sequence of numbers: $4,7,1,8,9,7,6,\dots$ For $n>2$, the $n$-th term of the sequence is the units digit of the sum of the two previous terms. Let $S_n$ denote the sum of the first $n$ terms of this sequence. The smallest value of $n$ for which $S_n>10,000$ is:

$\text{(A) }1992 \qquad \text{(B) }1999 \qquad \text{(C) }2001 \qquad \text{(D) }2002 \qquad \text{(E) }2004$

Solution

Problem 22

Triangle $ABC$ is a right triangle with $\angle ACB$ as its right angle, $m\angle ABC = 60^{\circ}$, and $AB = 10$. Let $P$ be randomly chosen inside $\triangle ABC$, and extend $\overline{BP}$ to meet $\overline{AC}$ at $D$. What is the probability that $BD > 5\sqrt{2}$?

$\textbf{(A)}\ \frac{2-\sqrt2}{2}\qquad\textbf{(B)}\ \frac{1}{3}\qquad\textbf{(C)}\ \frac{3-\sqrt3}{3}\qquad\textbf{(D)}\ \frac{1}{2}\qquad\textbf{(E)}\ \frac{5-\sqrt5}{5}$

Solution

Problem 23

In triangle $ABC$, side $AC$ and the perpendicular bisector of $BC$ meet in point $D$, and $BD$ bisects $\angle ABC$. If $AD = 9$ and $DC = 7$, what is the area of triangle $ABD$?

$\text{(A)}\ 14 \qquad \text{(B)}\ 21 \qquad \text{(C)}\ 28 \qquad \text{(D)}\ 14\sqrt5 \qquad \text{(E)}\ 28\sqrt5$

Solution

Problem 24

Find the number of ordered pairs of real numbers $(a,b)$ such that $(a+bi)^{2002} = a-bi$.

$\text{(A) }1001 \qquad \text{(B) }1002 \qquad \text{(C) }2001 \qquad \text{(D) }2002 \qquad \text{(E) }2004$

Solution

Problem 25

The nonzero coefficients of a polynomial $P$ with real coefficients are all replaced by their mean to form a polynomial $Q$. Which of the following could be a graph of $y = P(x)$ and $y = Q(x)$ over the interval $-4\leq x \leq 4$?

2002AMC12A25.png

Solution

See also

2002 AMC 12A (Problems • Answer Key • Resources)
Preceded by
2001 AMC 12 Problems 		Followed by
2002 AMC 12B Problems
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2002_AMC_12A_Problems&oldid=117988"