Difference between revisions of "Stewart's Theorem"
Happyhuman (talk | contribs) (→Proof) |
Happyhuman (talk | contribs) (→Proof) |
||
| Line 16: | Line 16: | ||
However, | However, | ||
<math>m+n = a</math> so | <math>m+n = a</math> so | ||
| − | + | <cmath>m^2n + n^2m = (m + n)mn = amn</cmath> and | |
| − | <cmath>d^2m + d^2n = d^2(m + n) = d^2a</cmath> | + | <cmath>d^2m + d^2n = d^2(m + n) = d^2a.</cmath> |
This simplifies our equation to yield <math>c^2n + b^2m = amn + d^2a,</math> or Stewart's Theorem. | This simplifies our equation to yield <math>c^2n + b^2m = amn + d^2a,</math> or Stewart's Theorem. | ||
Revision as of 15:27, 7 January 2020
Statement
Given a triangle ![]() with sides of length
with sides of length ![]() opposite vertices are
opposite vertices are ![]() ,
, ![]() ,
, ![]() , respectively. If cevian
, respectively. If cevian ![]() is drawn so that
is drawn so that ![]() ,
, ![]() and
and ![]() , we have that
, we have that ![]() . (This is also often written
. (This is also often written ![]() , a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")
, a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")
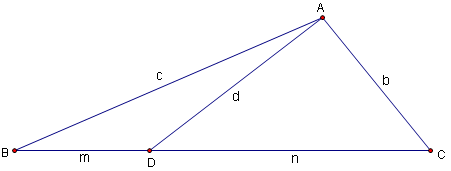
Proof
Applying the Law of Cosines in triangle ![]() at angle
at angle ![]() and in triangle
and in triangle ![]() at angle
at angle ![]() , we get the equations
, we get the equations
Because angles ![]() and
and ![]() are supplementary,
are supplementary, ![]() . We can therefore solve both equations for the cosine term. Using the trigonometric identity
. We can therefore solve both equations for the cosine term. Using the trigonometric identity ![]() gives us
gives us
Setting the two left-hand sides equal and clearing denominators, we arrive at the equation: ![]() .
However,
.
However,
![]() so
so
![]() and
and
![]() This simplifies our equation to yield
This simplifies our equation to yield ![]() or Stewart's Theorem.
or Stewart's Theorem.









